Research
01 – NANOSCIENCE IS ASTRONOMICAL; MINIMIZING INFORMATION LOSS DURING DIMENSIONAL REDUCTION
A tablespoon of water literally contains more water molecules than there are stars in the universe. It is not an understatement to say that modeling chemical systems requires accounting for an astronomical number of molecules. Statistical mechanics, the mathematical theory behind modern chemical physics, is arguably the original “big data” science.
How should we appropriately model how these huge numbers of molecules behave, and how they self-organize into complex structures? The answer is to use coarse-grained, lower-resolution models. In mathematics, this is called dimensionality reduction. However, we can not just use any statistical method, we have to make sure our models still follow physics.
To address this, I have used information theory to develop a novel multi scale simulation workflow that systematically minimizes the information loss of coarse-grained models, and to make them as accurate and faithful to how the atoms in the molecules actually behave. This work was done in collaboration with industry partners at BASF and Dow and is part of the core simulation capabilities of the NSF BioPACIFIC Materials Innovation Platform.
Work:
- K. Shen, N. Sherck, B. Yoo, M. Nguyen, S. Kohler, J. Speros, K. Delaney, M. S. Shell, G. H. Fredrickson, Rapid screening of polymer phase behavior using molecularly-informed field theories and machine learning, In Preparation.
- K. Shen*, M. Nguyen*, N. Sherck, Sherck, B. Yoo, S. Köhler, J. Speros, K. Delaney, M. S. Shell, G. H. Fredrickson, “Surfactant-polyelectrolyte micelle structure and coacervation transitions studied with a molecularly-informed field theory,” Eur. Phys. J. E 2023, submitted. *Denotes equal contribution.
- K. Shen, M. Nguyen, N. Sherck, B. Yoo, S. Kohler, J. Speros, K. Delaney, M. S. Shell, G. H. Fredrickson, Predicting surfactant phase behavior with a molecularly informed field theory, J. Colloid and Interface Sci. 2023, 638, 84-98
- M. Nguyen, N. Sherck, K. Shen, C. E. R. Edwards, B. Yoo, S. Kohler, J. Speros, K. Delaney, M. S. Shell, G. H. Fredrickson, Predicting Polyelectrolyte Coacervation from a Molecularly Informed Field-Theoretic Model, Macromolecules 2022, 55, 21, 9868–9879.
- N. Sherck, K. Shen, M. Nguyen, B. Yoo, S. Kohler, J. Speros, K. Delaney, M. S. Shell, G. H. Fredrickson, Molecularly Informed Field Theories from Bottom-up Coarse-Graining, ACS Macro Lett. 2021, 10, 5, 576–583.
Skills and tooling:
- python, numpy, pandas, pytorch, C++, CUDA
- cheminformatics, machine learning
- high dimensional numerical optimization
- molecular simulation: OpenMM (molecular dynamics), PolyFTS (field theory)
- contributed to coarse graining software package
- thermodynamics and molecular modeling
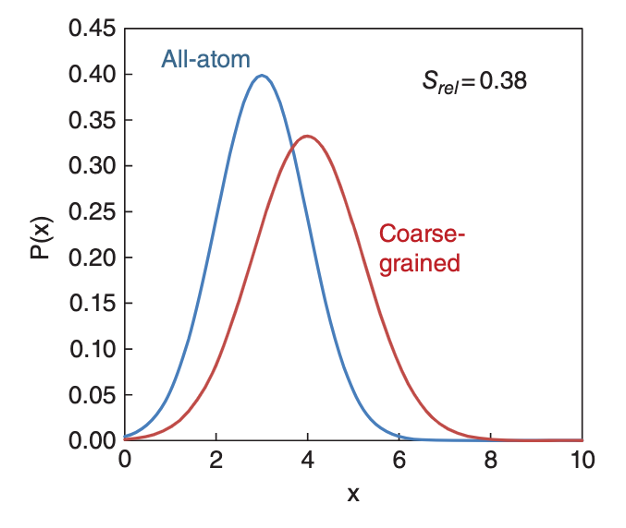
Fig. 1. A visualization of the relative entropy (“information loss”) of a 1D probability distribution. The closer the low-resolution, coarse-grained model distribution (red) matches the all-atom (blue) behavior, the better the model. We do this same procedure, but on a 100,000-dimensional molecular system.
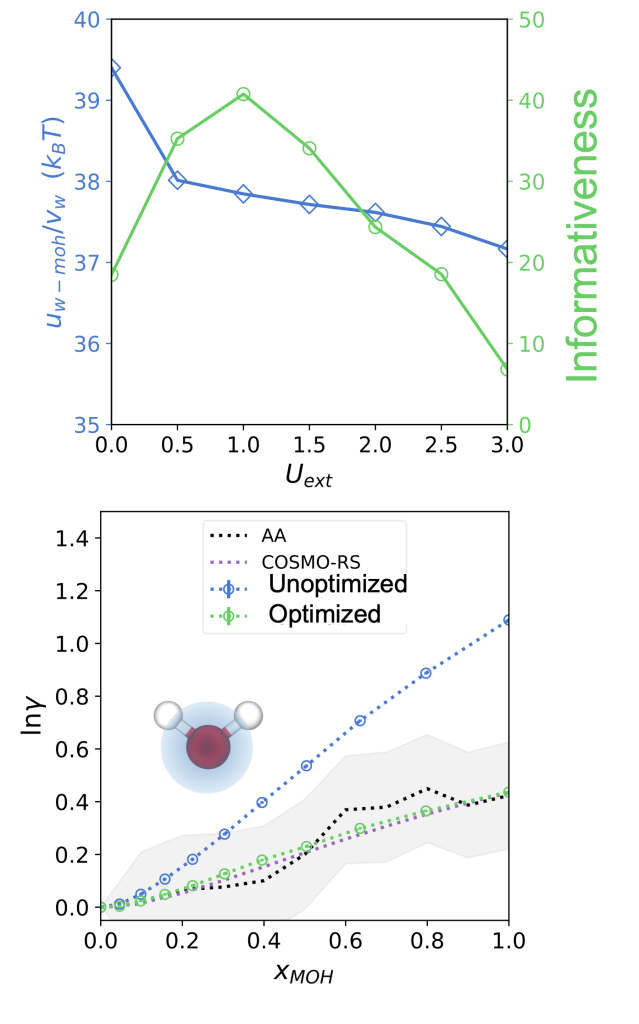
In this case study, we increase the information content of all-atom simulations by optimizing the application of a sinusoidal potential. The result is a coarse-grained model that matches the all-atom model (and the empirical COSMO-RS model) across all compositions.
02 – TRANSFER LEARNING
One of the perennial problems in any kind of modeling is understanding the extent of model validity. I.e., can your model extrapolate beyond the initial data set that it is trained upon? The more extrapolative your model, the more broadly applicable it is.
This transferability challenge has plagued molecular modelers for decades. The result is that new models usually need to be specifically tailored every time new molecules are introduced. Sometimes, even if the ingredient molecules remain the same, the model only works at certain mixing fractions (say, 50/50) but not at other compositions (say, 20/80)! Even worse, standard techniques to build coarse-grained models oftentimes get the miscibility and incompatibility between molecules wrong, limiting their predictive power.
I demonstrated that an extension of the Fisher Information has direct physical interpretation in molecular systems, and correspondingly the information content of a molecular simulation can be manipulated via physical manipulations like applying external potentials. Additionally, the Fisher Information can be a reliable and cheap measure of model quality. For the first time, I demonstrated that one can actually systematically optimize the data collected for building molecular models.
Work:
- K. Shen, N. Sherck, M. Nguyen, B. Yoo, S. Kohler, J. Speros, K. Delaney, M. S. Shell, G. H. Fredrickson, Learning composition-transferable coarse-grained models: Designing external potential ensembles to maximize thermodynamic information, J. Chem. Phys. 2020, 153, 154116 (2020). Editor’s Pick.
Skills and tooling:
- Information theory, statistical learning, statistics
03 – STATISTICAL MECHANICAL THEORY
Statistical mechanics is about calculating the probability distribution of expected molecular behaviors. The challenge, of course, is that molecular probability distributions have a ginormous number of dimensions.
During my PhD, I developed a mathematical approach to greatly simplify the calculation of these high-dimensional probability distributions. The nice thing? It wasn’t just lines and lines of math. The math actually gave a new description and picture of understanding how the shape of molecules responds to and changes their environments, in a delicate give-and-go and is now a key part of modern models of polyelectrolytes (charged polymers).
Work:
- P. F. Zhang, K. Shen, N. M. Alsaifi, Z.-G. Wang, Salt partitioning in complex coacervation of symmetric polyelectrolytes. Macromolecules 2018, 51, 15, 5586–5593.
- K. Shen, Z.-G. Wang. Polyelectrolyte Chain Structure and Solution Phase Behavior. Macromolecules 2018, 51, 5, 1706–1717.
- K. Shen, Z.-G. Wang. Electrostatic correlations and the polyelectrolyte self energy. J. Chem. Phys. 2017, 146, 084901 (2017). Editor’s Choice. (One of 73 articles selected from the journal for the entire year).
Skills and tooling:
- object oriented programming, python, matlab
- variational calculus, statistical mechanics
